先日の記事では、中秋の名月を眺める楽しみ方や観測の方法をご紹介しました。天体観測は「美しい光景を楽しむ」だけでなく、その裏側に潜む法則を知るとさらに奥深い世界が広がります。今回は、前回取り上げた月の満ち欠けを「数学的に」考えてみましょう。
月の満ち欠けを周期で表す
月はおよそ29.53日周期で満ち欠けを繰り返します。この周期を「朔望月(さくぼうげつ)」と呼びます。つまり、ひと月ごとに「新月 → 上弦 → 満月 → 下弦 → 新月」というサイクルをたどるのです。
この変化を数式で表すと、実は三角関数が登場します。たとえば、月の明るさを「0(新月)」から「1(満月)」の間で表すと、次のような近似式で書くことができます。
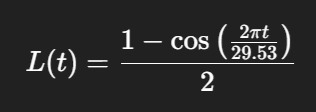
ここで ttt は新月からの日数、L(t)L(t)L(t) は明るさの割合です。この式から、なぜ満月は「丸1日」しか見られないのに、半月はしばらく続くのか、といった直感的な違いも説明できます。
数学で予測する「次の満月」
たとえば、9月8日が満月だとわかれば、その29.53日後、つまりおよそ10月7日が次の満月だと数学的に予測できます。実際の天文学でも、非常に精密な三角関数や楕円軌道の計算を組み合わせて「月齢カレンダー」が作られています。
こうした仕組みを知ると、ただ「満月だ!」と喜ぶだけでなく、「次の満月はこの日だ」と数学的に推測しながら夜空を見上げられるようになります。
円と角度で見る月の形
もう一つ、数学が活躍するのが「月の見え方」の説明です。
地球から見た月の形は、太陽と月と地球の位置関係によって決まります。地球を中心とした円の上に月が動いていると考えると、角度 θ\thetaθ に応じて見える部分の割合が計算できます。
単純化すると、地球から見える月の形は「円の一部が照らされている状態」で、これは「扇形」と「レンズ型の図形」の重なりとして計算できます。小学校で習った「円の面積の公式」や「三角比」がそのまま応用されているのです。
美しさと法則をつなぐ
このように、月の美しい満ち欠けには「周期」「三角関数」「円の幾何学」といった数学が隠されています。夜空を見上げるとき、ただ目で楽しむだけでなく「今の明るさはどのくらいか」「この形は何日後の数式で説明できるか」と考えると、天体観測が知的な遊びに変わります。
月齢カレンダーおすすめグッズ
| 商品名 | 形式 | 特徴 | おすすめ用途 |
|---|
| 2026年 月齢・月の満ち欠けカレンダー | 壁掛けカレンダー | 1年分の月齢一覧 | 来年の観測予定 |
| 月齢暦2026 | 暦 | 翌年版 | 長期観測 |
| CASIO スタンダード ムーンフェイズ 腕時計 | 時計 | 文字盤に月の満ち欠け表示する月相表示機能 | 日常使い・ガジェット |
🌕 まとめ
中秋の名月という美しい現象も、数学の視点で見ると「周期の調和」として新しい姿を現します。自然と数学がつながる瞬間を味わいながら、ぜひ次回の観測で「数式と夜空」を一緒に楽しんでみてください。



コメント